廊下を曲がれる棒の長さに関する問題
高校の時に目にした数学の問題で、ずっと印象に残っているものがあった。多分「大学への数学」かその別冊に載っていたのだと思う。自分で解いたことはなかったし、答も全く覚えていなかったのだが、最近ふと思い立って、ちょっとカンニングしながらも解を導くことができた。日本語のサイトで解法を書いてあるページを見かけない(答を書いてあるページはあるが)ので、ここに書いておく。
問: 幅
の廊下から幅
の廊下へ直角に曲がる曲がり角がある。この曲がり角を水平に持って曲がれる棒の長さの最大値を求めよ。
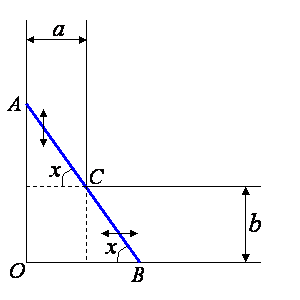
図のような曲がり角を通っていくことのできる棒の長さは最大どれだけかという問題である。
【解答】
曲がり角をギリギリで曲がろうとすると、下図のように棒の両端A, Bを壁につけ、途中を曲がり角Cに当てた状態で動かすことになる。動かしている間中ずっと棒は廊下におさまっていないといけないから、このような状態で棒の長さを可変と考え、棒を傾けていったときのABの長さの最小値を求めればよい。
角OBAをとすると、棒ABの長さは
の関数
で表せる。
、
であるから
求める長さは、の範囲での
の最小値ということになる。
の範囲では
と
は常に正で、
が
に近づくとき
は
に、
は
に近づく。
が
に近づくとき
は
に、
は
に近づく。したがって
が
に近いとき
は負になるから
は減少し、
が
に近いとき
は正になるから
は増加する。途中
となる
を
とすると、そこで
は最小となり、求める長さは
である(このあたりは増減表を書いてみるとわかる)。
よってのとき、
,
であることと
を使って
したがって
,
これらとの定義式から、求める長さは
結構きれいな式になるものである。のとき
(45度)、
となる。
,
の片方が他方に比べ極端に大きいときは、曲がり角でほとんど回転できないため、大きい方に近い値(広い方の廊下の幅に近い長さ)になる。